In recent years, the Maritime Research Institute Netherlands (MARIN) investigated the potential of a Rankine source code to predict the added resistance of ships in waves. In addition to investigation of accuracy issues inherent to the measured wave added resistance, the research also revealed an unexpected large effect of the voluminous bulbous bow.
The subject of added resistance in waves has got more attention for various reasons. First of all, to ascertain the safety of vessels in harsh conditions. The (to be) lowered installed power requirement following the IMO Energy Efficiency Design Index (EEDI) regulation could potentially conflict with the Minimum Power Requirement regulations.
Second, the eventual introduction of concrete emission based regulation (Energy Efficiency Operational Indicator (EEOI) using Monitoring, Reporting and Verification of CO2 emissions (MRV) or the IMO Data Collection System on fuel consumption (IMO DCS)) will focus on the ships’ operational capabilities. The latter being seriously affected by the added resistance in waves vessel characteristics. As a bulbous bow goes well with a full block ship and the latter becoming more popular with ship speeds decreasing, they both add to the added resistance in waves.
The fact that for some ship types the prediction with MARIN’s Rankine source code [1] showed a poor correlation with results from seakeeping tests led, in addition to accuracy issues in the code and in the experiments, to the discovery of an unexpected large role of a voluminous bulbous bow in the added resistance. This finding, and the fact that in this case the added resistance does not follow the expected trend with the square of the wave amplitude, was confirmed with Computational Fluid Dynamics (CFD) calculations.

Physics
An enabling factor that magnifi es the effect of the bulb is that the over-all added resistance is the relatively small sum of a large aftward force acting along the waterline and a number of forward acting forces among which the “suction” due to a second-order pressure drop over the mean submerged part of the hull. This makes it sensitive to relatively small changes in either of the two components. Figure 1 illustrates this character for the KCS container ship hull; the total added resistance is some fifty per cent of the “waterline contribution”.
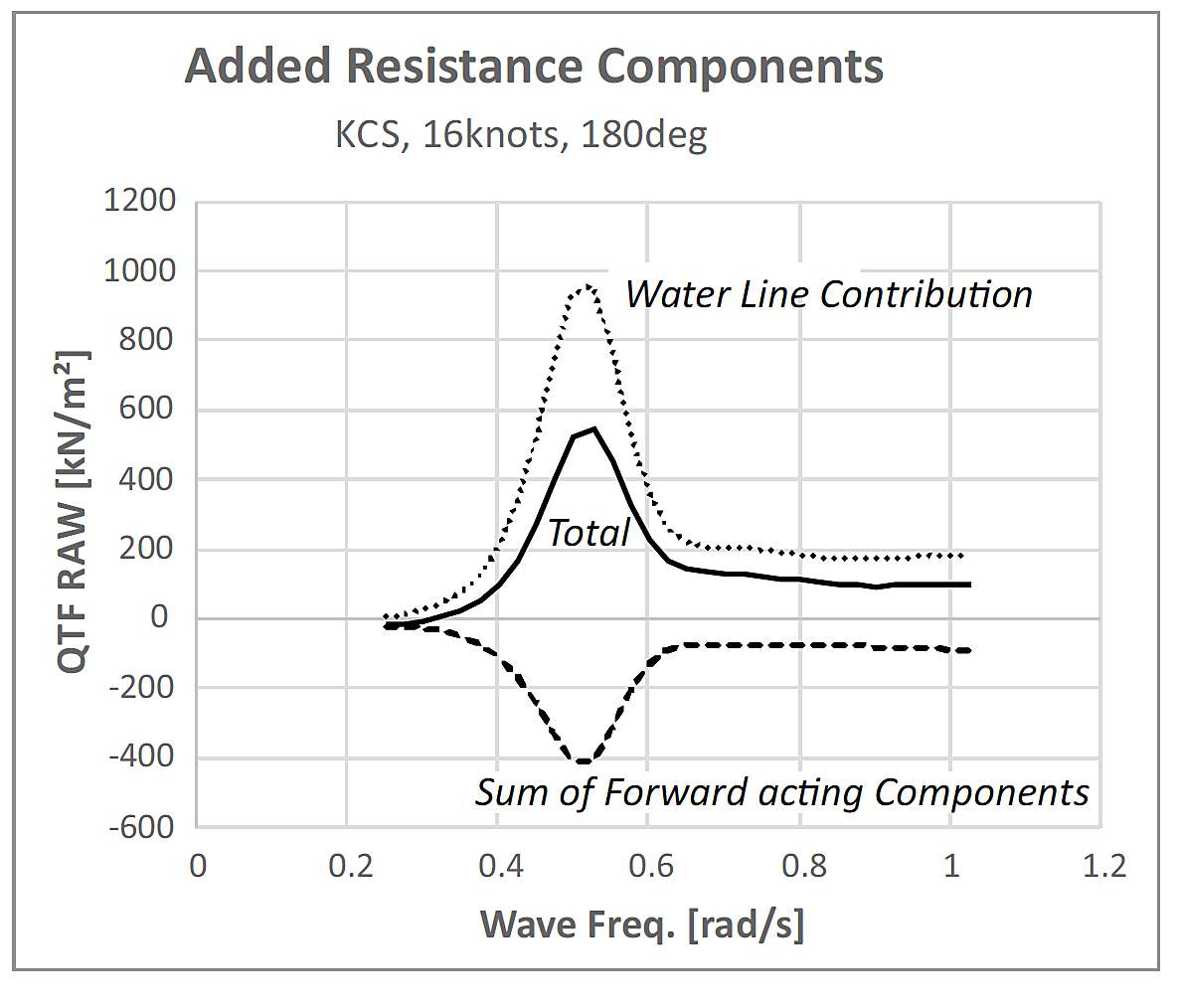
Figure 1. FATIMA estimate of the quadratic transfer function of the added resistance of the KCS container ship hull in regular head waves. The KCS container ship is a publicly well documented vessel used within many studies.
The prime factor in the bulb’s effect is a change in the relative wave elevation in the diverging flow at the bow, see figure 2. The impact is magnified by the fact that the resulting waterline contribution in the added resistance is governed by the square of this quantity.
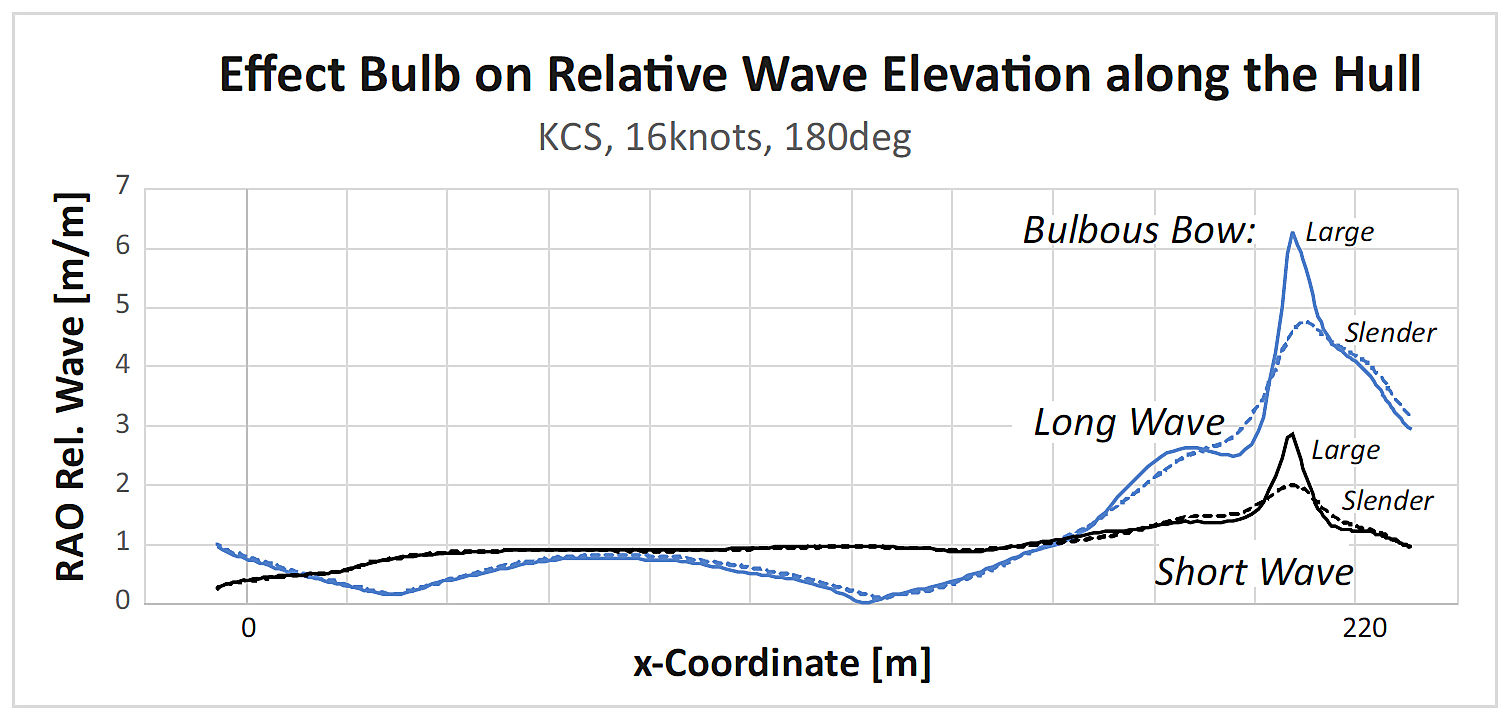
Figure 2. Effect of bulbous bow on the amplitude of the relative wave elevation along the hull.
Validation
A dedicated series of experiments with a six-metre model of the well-known KCS container ship was used to check the results of the calculations. In order to improve accuracy, a constant forward speed was enforced by towing the model by means of a flexible rod. Using the “follow-mode” of the towing carriage in the transverse direction, this semi-captive set-up allows tests with a self-steering, largely self-propelled model in waves from an arbitrary direction.
In the analysis, the added resistance is obtained by subtracting the value of the sum of the mean values of the effective propeller thrust and the tow force obtained in calm water from the value in waves. Division by the square of the amplitude of the undisturbed incident wave yields the quadratic transfer function (QTF) of this quantity.
Because of uncertainties regarding the repeatability of the calm water references, the tests in calm water and in waves were performed in pairs at each wave frequency; figure 3 indicates the resulting resistance estimates. The first three tests in short waves, where the added resistance is low, make it clear that an accurate assessment is not a trivial matter.
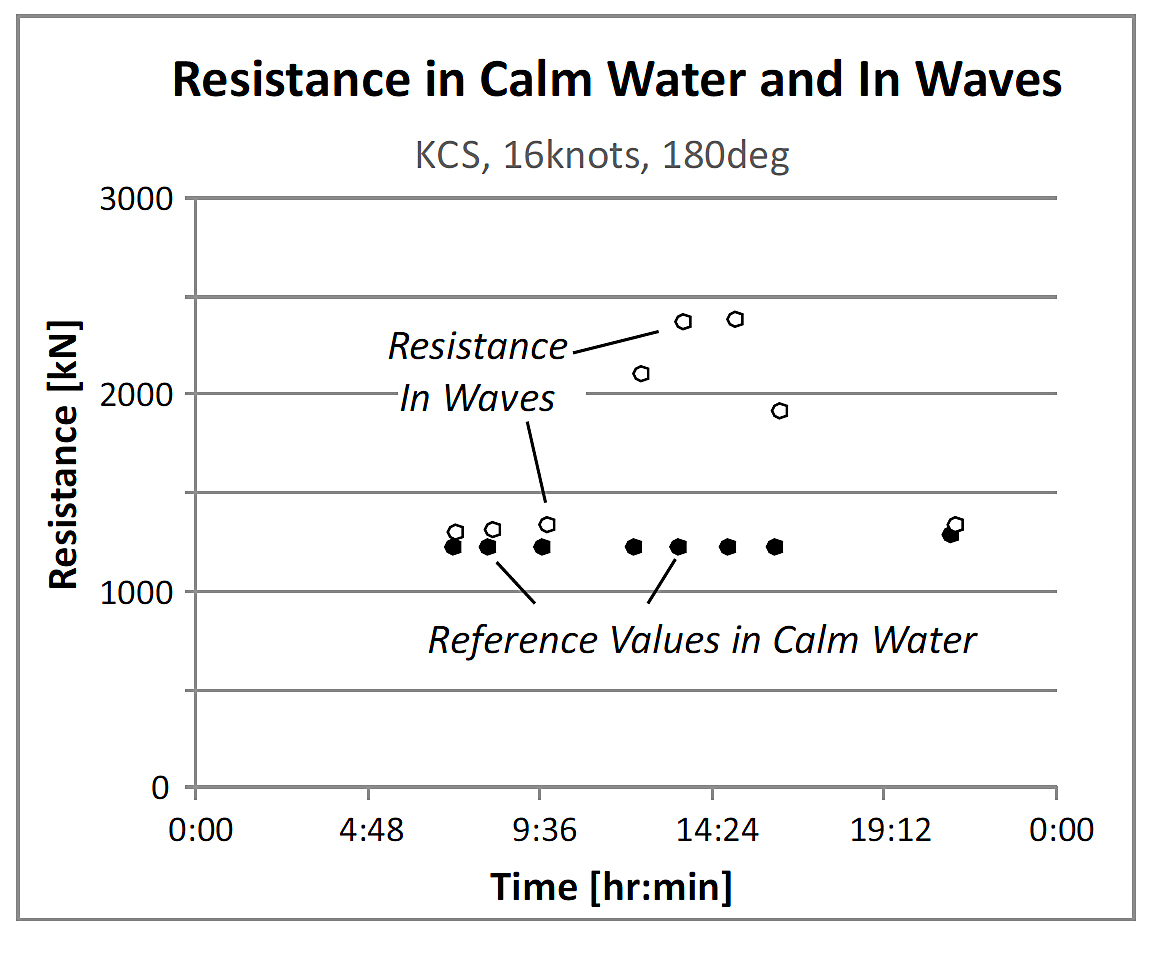
Figure 3. Resistance estimates from a sequence of tests in calm water and in waves.
In the derivation of the added resistance, a resistance estimate in waves can be combined with any of the values in calm water. Figure 4 shows that the resulting set of QTFs agrees well with the result that is obtained when using the time-local value as a reference. A comparison of the results of the experiments with the results of the potential flow calculations (the code used for this is called FATIMA) shows an encouraging correlation, except for the peak value. The poor agreement around the peak was the subject of a number of additional tests in which the wave amplitude was varied.
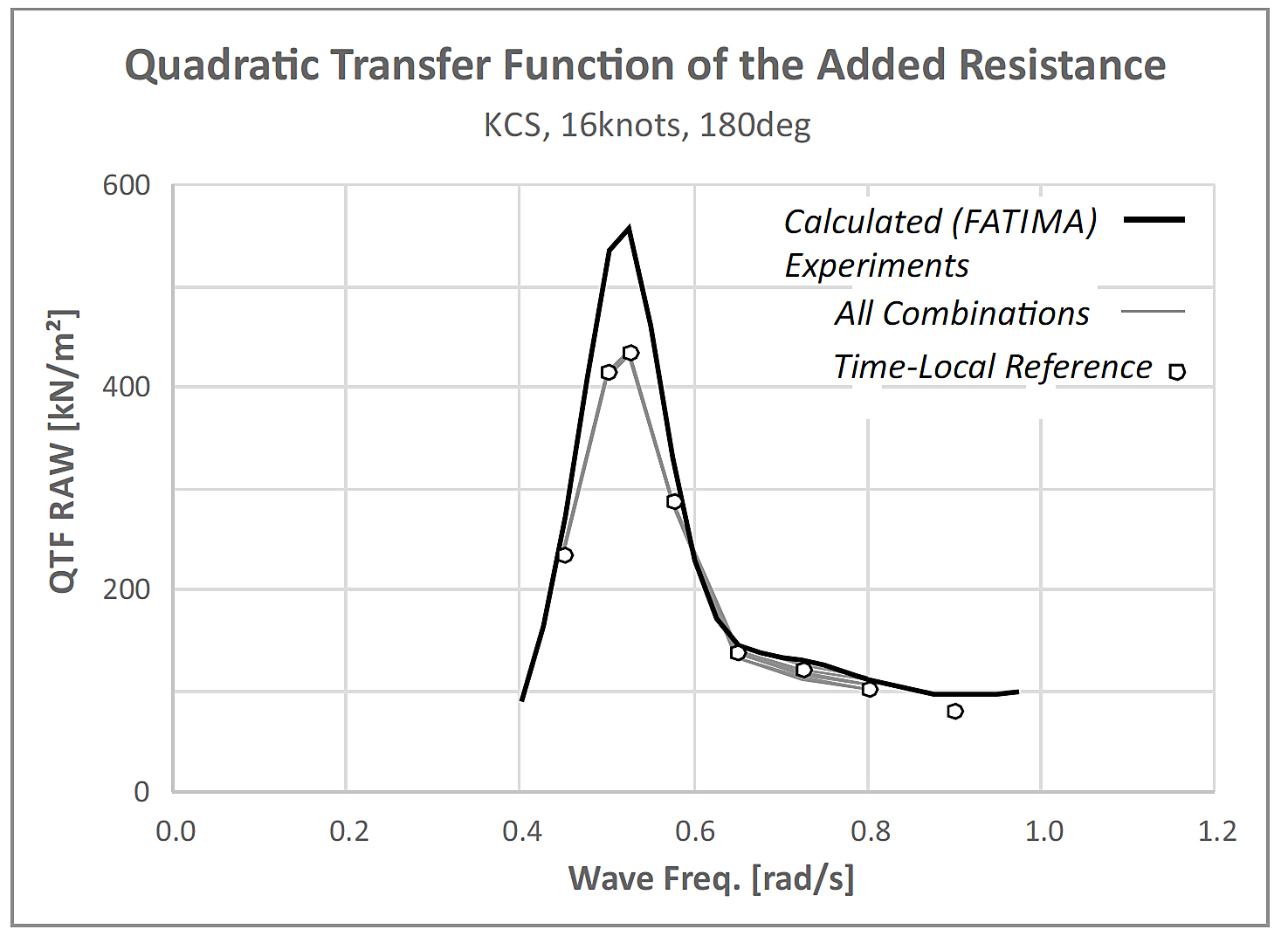
Figure 4. Quadratic transfer function of the added resistance in head waves.
In addition, CFD calculations were performed. The results in figure 5 show that in the low wave amplitude range, the CFD and (FATIMA) potential flow results show the same trend. The CFD and the results of the experiments agree on the fact that in higher waves, the values drop substantially. At the lowest amplitude, the experiment lacks the resolution that is required to capture the trend.
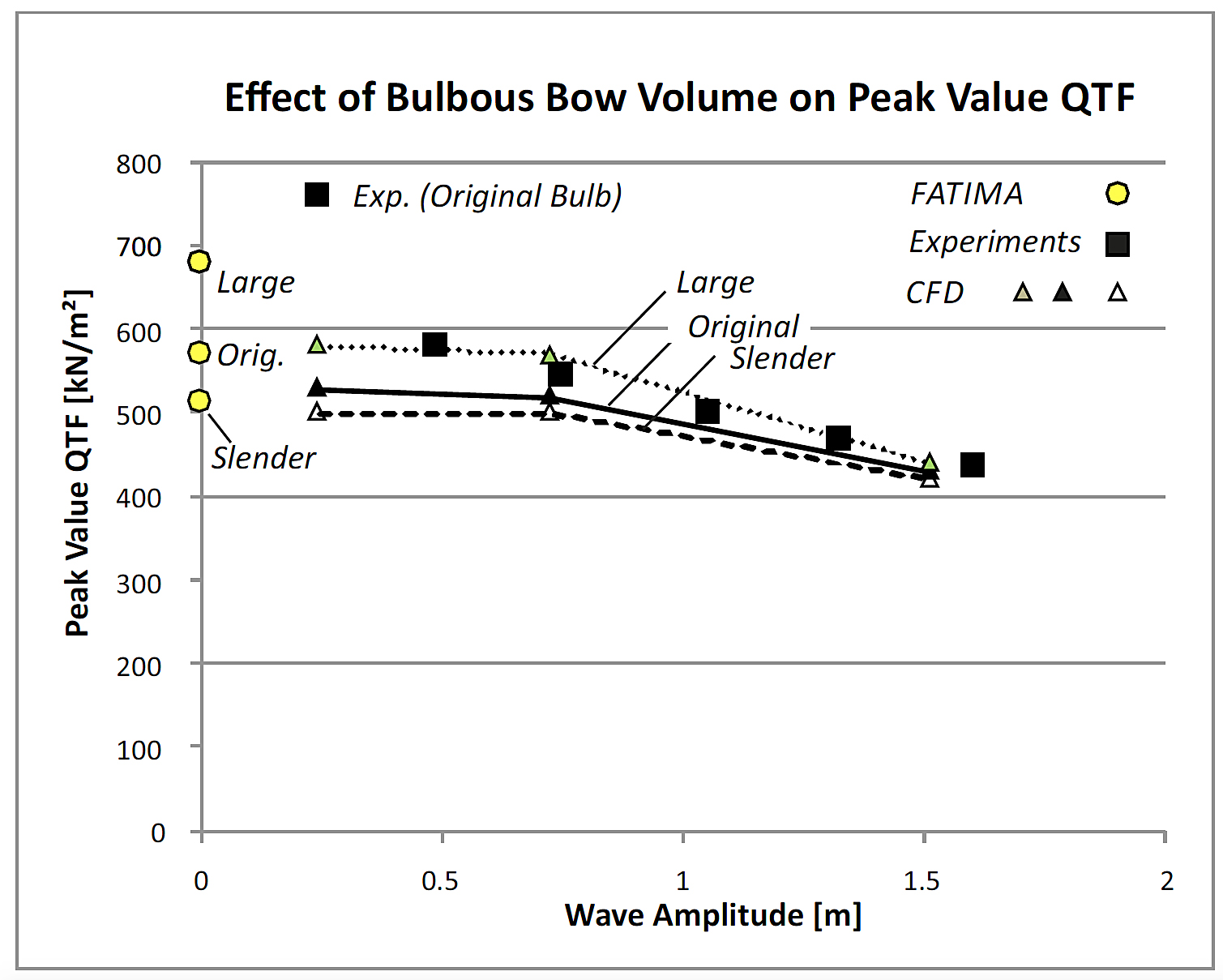
Figure 5. Effect of wave amplitude and bulb size on the peak value of the QTF.
Figure 5 also shows CFD results for two additional bulb arrangements. They confirm that the largest bulb yields a relatively high added resistance in the lower wave height range. In higher waves the effects of the bulbous bow diminish. The results imply that the design of a bulb is a compromise between its benefits in calm water and a penalty in waves which depends on the target route.
Figure 6 visualises the location of the added resistance with a plot of the change in the time-average longitudinal force over the fore body of the subject vessel. The results are normalised with the square of the amplitude incident wave. The amount of detail in the “pressure” distribution in low waves seems to reflect the interaction of the steady and unsteady flow components as obtained in potential flow calculations. In higher waves these details, and the interaction of the wave components, largely disappears.
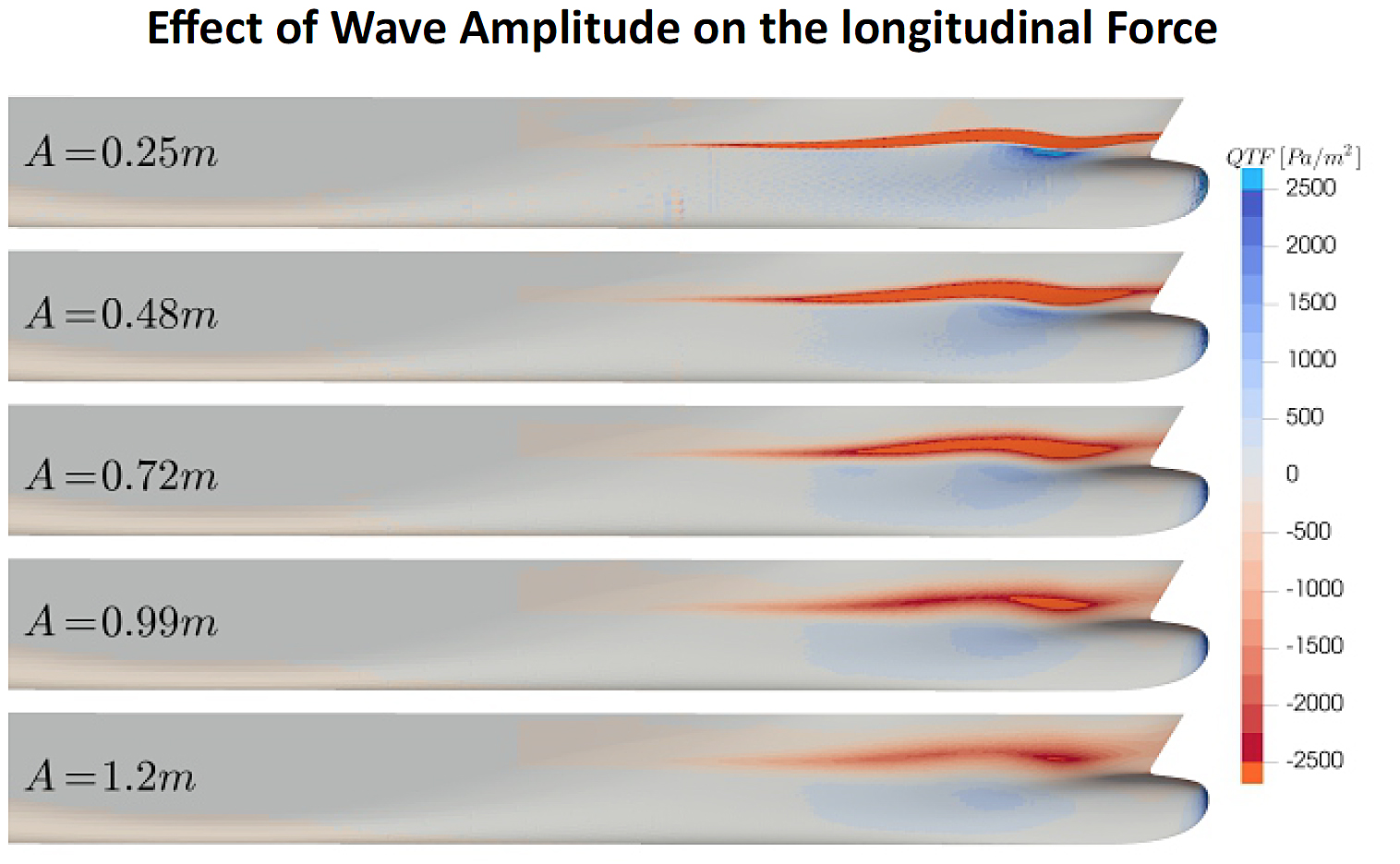
Figure 6. Effect of wave amplitude on the mean longitudinal force acting on the hull.
Added resistance can now be predicted
The present understanding of the numerical shortcomings of the FATIMA code, in combination with experiments with special attention for the accuracy and contemporary CFD have largely resolved the problem of predicting the added resistance of a ship in regular waves. The combination of an efficient potential flow code and accurate CFD yields a sound basis for an evaluation of fuel consumption and involuntary speed loss for the wide range of wave conditions that are encountered during operation at sea.
Picture (top): KCS model during the experiments.
References
- Bunnik, T.H.J. 1999. Seakeeping calculations for ships, taking into account the non-linear steady waves. PhD Thesis, Delft University of Technology, the Netherlands.
- Crepier, P., Rapuc, S. and Dallinga, R.P., CFD Investigation into the Wave Added Resistance of Two Ships, PRADS 2019
This article was kindly supplied to SWZ|Maritime by MARIN and published in our January 2020 issue. It was written by: